EŞİTSİZLİKLER 1
|
Aralık Kavramı:
Şeklinde
olur. |
|
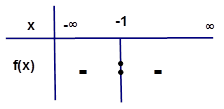
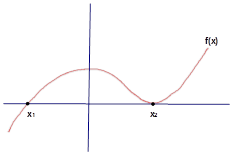
NOT1:
Yandaki
grafikte
|
|
NOT2: NOT1
deki işaret tablosunda
|
|
TANIM:
|
|
NOT3:
Eşitsizliğin çözüm kümesini bulmak için
|
|
NOT4: Çözüm aralığını bulduktan sonra köklerin denklemi sağlayıp sağlamadığı kontrol edilip, çözüm kümesine eklenip çıkarılacağı üzerine yorum yapılır.
|
|
Örnek1: Çözüm:
Sıfırdan
küçük olan yerler x=-2 ve x=5 denklemi sağlamaz deriz ve bu yüzden açık parantez kullanılır. (bkz not4)
|
|
Örnek2: Çözüm:
Çözüm
kümesi
|
|
Örnek3: Çözüm:
İfade İşaret tablosu da aşağıdaki gibi olur.
Görüldüğü
gibi Şimdi de kökleri inceleyelim (bkz not4) x=2 için
|
|
|
|
Örnek4: Çözüm: Her çarpanın kökünü bulalım.
Kökleri de incelersek paydayı sıfır yapan x=3 çözüm kümesine eklenmez x=2 ve x=1 denklemi sağlar bu yüzden
Dikkat: Burada önemli olan x=3 ün sağında yani 3 ten büyük değerler için fonksiyonun pozitif değerler aldığını görmektir. Bunun için x yerine 3 ten büyük bir değer verilebilir veya daha kısası ifadede her bir çarpanın başkatsayısının işaretlerini çarpmaktır. Yani x-2 nin başkatsayısı 1 dir, işareti de + dır x-1 in başkatsayısı 1 dir ve işareti + dır. x-3 ün başkatsayısı 1 dir ve işareti + dır. 3 adet + işaretinin çarpımı + olduğundan tablonun en sağı + ile başladı.
|
|
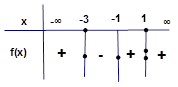
Örnek5: Çözüm:
Görüldüğü gibi x=1 den iki kök (yani çift kat oldu) x=-1 den ve x=-3 ten birer kök var. Burada önemli olan x=1 kökünün iki çarpanda olduğunu görüp çift kat olarak tabloya eklemektir. Başkatsayının işaretlerine bakarsak hepsi + olduğundan en sağ + ile başlar.
x=1 çift kat kök olduğundan işaret değiştirmedik. Şimdi kökleri inceleyelim. x=-3 paydayı sıfır yaptığından ç.k ne eklenmez. x=-1 ve x=1 pay kısmında ve eşitlik olduğu için eşitsizliği sağlar ve ç.k ne eklenir. Bizden
|
|
Örnek6: Çözüm: kökleri bulalım.
x=1 den ilk çarpanda 2015 tane, ikinci çarpanda da 1 tane var. Dolayısıyla x=1 çift kat köktür.(2015+1=2016 çift sayı) x=-1 den ise 1 kök vardır o yüzden tek kat köktür. İşaret tablosunu yapalım.
Kökler eşitsizliği sağlamadığından ç.k ne dahil edilmez.
|
|
*Örnek7: Çözüm: Her zamanki gibi kökleri bulalım.
Başkatsayıların işaretlerine baktığımızda en sağ negatif işaretli olur. ( Kökleri
incelersek, x=-1 denklemi sağlar. Bizden
|
|
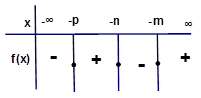
Örnek8:
Çözüm8: Her zamanki gibi kökleri bulalım. x+m=0 ise x=-m, x+p=0 ise x=-p ve x+n=0 ise x=-n olur. işaret tablosunda kökleri küçükten büyüğe yerleştireceğiz. (m=-1, n=1 ve p=2 alınırsa 'm=1, -p=-2 ve 'n=-1 olur. -2<-1<1 olduğundan 'p<-n<-m olur. İşaret tablosunun en sağı için katsayıların işaretlerine bakarsak tüm başkatsayılar 1 dir, demek ki en sağ + dan başlayacak.
kökleri
incelersek paydada olan 'n denklemi sağlamazken, pay kısmında olan 'm ve -p
eşitik olduğu için denklemi sağlar. Bizden
|

Basit Eşitsizlikler

Eşitsizlikler - 2
Yapılan Yorumlar
Sabahtan beri böyle bir anlatım arıyorum, her yerde saçma saçma şeyler çıkıyor burası çok iyi. Çok teşekkürler :D
Çok güzel anlatmışsınız allah razı olsun
Siirtte yazıyorun yarın sınavım var. Emeği geçen herkese teşekkürler.
Berbat anlatım beğenmedim
Cok iyi👊 gercekten begendim
Çok yardimci oldunuz
Gercekten anlamak isteyen varsa anlar...haarika anlatmissiniz tesekkurler
Iyi
Cok guzel
Cok tesekkurler universite ogrencisiyim isime yaradi
Cok tesekkurler universite ogrencisiyim isime yaradi
İyi bir sunum
Ben matematikçiyim bana bile yaradı :)
Allah razı olsun, güzel bir anlatım olmuş.
Bence sade ve ogretici
Teşekkürler. Gayet sade ve güzel
teşekkürler
Alese hazırlanıyorum çok teşekkür edrim 👌🏻
Fonksiyon grafigiyle esitsizlik ornekleri olsaydi daha guzel olurdu.Ama yine tesekkurler guzel anlatım
Gerçekten güzel anlatım soru çeşitleriyle daha iyi öğrendim
2023'ten selamlar efenim,
Not: seçimin ikinci tura kaldığı dönem
Yorum Yapın
- EBOB - EKOK - 2 121493 ziyaret
- İşçi Problemleri 298784 ziyaret
- Eşitsizlikler - 2 80927 ziyaret
- Sayı Kesir Problemleri - 2 59614 ziyaret
- Karmaşık Sayılar 109892 ziyaret
- Eşitsizlikler - 2 17 dakika önce
- EBOB - EKOK - 2 30 dakika önce
- İşçi Problemleri 53 dakika önce
- Faktoriyel 1 saat önce
- 2. Dereceden Denklemler - 1 1 saat önce
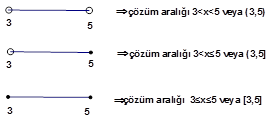


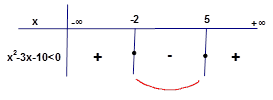 Çarpanlarına ayırırsak
Çarpanlarına ayırırsak 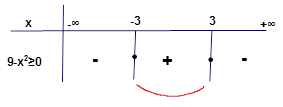
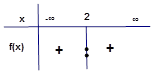
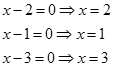
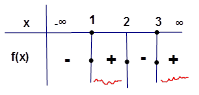
 Başkatsayıların işaretleri çarpımı + olduğundan en
sağ + ile başlar.
Başkatsayıların işaretleri çarpımı + olduğundan en
sağ + ile başlar.