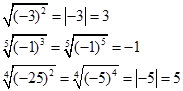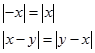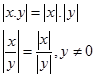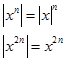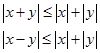MUTLAK DEĞER 1
AÇIKLAMA: Öğrenci arkadaşların zorlandığı konulardan biri de mutlak değer konusudur. Bu konuda dikkat edilmesi gereken şey mutlak değerin uzunluk olduğudur.
Tanım: x, gerçel sayı olsun. X sayısının başlangıç noktasına
olan uzaklığına (ki bu nokta sayı doğrusunda 0 (sıfır)dır) x in mutlak değeri denir,
ve ![]() ile gösterilir.
ile gösterilir.
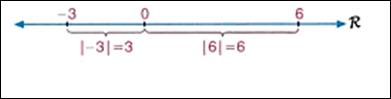
Yukarıdaki şekilde
(-3) ve (6) sayılarının 0'a olan uzaklıkları gösterilmiştir. (-3) sayısının
uzaklığı 3 ve 6 nın uzaklığı da 6 dır.
![]() ,
, 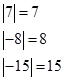
|
Örnek1: . .
|
mutlak değerin içi belli iken sayıyı mutlak değer dışına pozitif olarak çıkartıyoruz.
Mutlak değerin içi bilinmeyen bir ifade olduğunda da aynı işlemi yapacağız. Ama önce şu soruya cevap verelim.
!
(![]() ) pozitif bir sayımıdır negatif
bir sayı mıdır? Cevap: bilinmez. Çünkü;
) pozitif bir sayımıdır negatif
bir sayı mıdır? Cevap: bilinmez. Çünkü;
1.durum: x negatif bir sayı ise önüne eksi aldığı için pozitif olur.
2.durum:x pozitif bir sayı ise önüne eksi aldığ için negatif olur.
Not: mutlak değerin içinin pozitif olduğunu bildiğimiz durumlarda mutlak değerin içinde ne varsa olduğu gibi çıkartacağız. Mutlak değerin negatif olduğunu bildiğimiz durumlarda da mutlak değerin içindeki ifadeyi (-1) ile çarpıp çıkartacağız.
|
Örnek2:
Çözüm:1.mutlak değerin içinde Benzer şekilde 2. mutlak değerli ifadeyi incelediğimizde büyük
sayıdan küçük sayı çıkartılmış o yüzden mutlak değerli ifadeyi olduğu gibi
çıkartacağız. (
|
|
Örnek3: Çözüm: x negatif olduğu için önüne (-) alarak çıkacak.
|
|
Örnek4: Çözüm 4: X negatif, y pozitif ise ise X negatif olduğu için sonuç;
|
not: ![]() olmak üzere
olmak üzere
 olur.
olur.
Mesela;  ,
,
 ,
, 
|
Örnek5:
|
|
Özellikler.
|
!
![]() . (
. (![]() )
)
![]() veya
veya ![]()
![]()
Not:mutlak değer 2 konu anlatımında yukarıda verdiğim ünlemin içeriği ile ilgili sorular çözeceğiz.
|
Örnek6: Arkadaşlar iki mutlak değerin (uzunluğun) toplamı nasıl sıfır olur. bunun tek şart iki mutlak değerin de sıfır olmasıdır. Yani ;
|
Dikkat: ![]() olur.
olur.
|
Örnek7:
Dikkat: A denkleminde yerine konur. Çıkan küçük değer cevabımızdır. (nedeni LYS fonksiyon çizimlerinde anlatılacaktır.) Sorumuza dönersek;
|

Mutlak Değer - 2
Yapılan Yorumlar
Teşekkür ederim.
Cok ıyı:):):)
Gayet açıklayıcı bir anlatim :)
Coook iyi
😀😁
Teşekkür ederim
Anlatımını gayet açıklayıcı olmuş
super hocammmmmmmmmmm
Süper! Gerçekten çok iyi
Nasıl olduğunu anlamadım
sınıf 2.si olarak çok iyi anlarım matamatikten süper
teşekürler
hiç bişey anlamadım
emeyinize sağlık
Çok iyi yazmışsınız
Teşşekür ederim elinize emeğinize sağlık 😊
emeğinize sağlık
Yorum Yapın
- İşçi Problemleri 298901 ziyaret
- EBOB - EKOK - 2 121548 ziyaret
- Yüzde Problemleri - 2 (Kar - Zarar Problemleri) 323491 ziyaret
- Yüzde Problemleri - 1 60821 ziyaret
- Karmaşık Sayılar 109928 ziyaret
- Yüzde Problemleri - 1 5 dakika önce
- Eşitsizlikler - 1 8 dakika önce
- Eşitsizlikler - 2 28 dakika önce
- Yüzde Problemleri - 2 (Kar - Zarar Problemleri) 30 dakika önce
- İşçi Problemleri 53 dakika önce