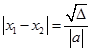2. DERECEN DENKLEMİN KÖKLERİ İLE KATSAYILARI ARASINDAKİ BAĞINTILAR
|
2. derece denklemlerde en önemli noktalardan biri köklerin katsayılar ile olan ilişkisidir. NOT: Kökler
toplamı (sebebini
bilelim:
Kökler
çarpımı: (sebebini
bilelim:
Kökler
farkı:
|
|
Örnek1: kökler
toplamı Kökler
çarpımı Kökler
farkı
|
|
Örnek2: Çözüm:
Kökler toplamı
|
|
Örnek3: Çözüm:
|
|
Örnek4: Çözüm:
|
|
Örnek5: Çözüm:
|
|
Örnek5: Çözüm:
|
|
Örnek6: Kökler
arasında Çözüm: Kökler
toplamının bulunur.
|
|
Örnek7: Kökler
arasında Çözüm: Kökler
çarpımının
|
|
Örnek8: Çözüm: Kökler toplamını ve kökler çarpımını yazalım. a ve b kök olduğundan, Kökler
toplamı Kökler
çarpımı
|
|
NOT: c ile 'c nin toplamının sıfır olduğuna dikkat edelim.
|
|
Örnek9: Çözüm: Simetrik iki kökün toplamı sıfır olduğundan ,
|

2. Dereceden Denklemler - 2
Yapılan Yorumlar
Çok iyiymiş yaaa
Çok saolun. Cümle kurarak anlatımınız çokk iyi olmuş
çok zor yaaa
BU NASİL BİŞİ ANLAMADLM
Gerçekten bütün örnekler var çok güzel
Biraz fazla olsa cok daha güzel olacakmış
hocam heykelinizi dikelim desek belden aşşaya beton yetmez :) çok güzel olmuş teşekkürler.
Emeginize sağlık
Yorum Yapın
- Yüzde Problemleri - 2 (Kar - Zarar Problemleri) 321370 ziyaret
- İşçi Problemleri 293410 ziyaret
- Karmaşık Sayılar 107941 ziyaret
- Basit Eşitsizlikler 39622 ziyaret
- Faktoriyel 503394 ziyaret
- Sayılar 1 dakika önce
- Sayılarla İlgili Karışık Örnekler 10 dakika önce
- Basit Eşitsizlikler 13 dakika önce
- İşçi Problemleri 17 dakika önce
- Polinomlar - 3 27 dakika önce