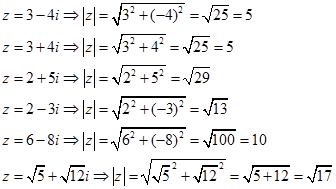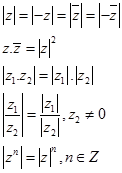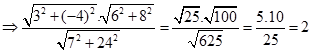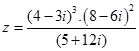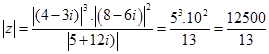KARMAŞIK SAYILAR 1
|
Şimdiye kadar bildiğimiz en geniş küme reel sayı kümesiydi. Şimdi reel sayıları da kapsayan bir küme ile tanışalım. Karmaşık Sayılar kümesi. C ile gösterilen bu küme,
Burada a sayısına reel (gerçek) kısım denir ve Re(z) ile gösterilir. b sayısına da sanal (imajiner kısım) denir ve Im(z) ile gösterilir.
|
|
Örnek: Z=2+3i karmaşık sayısının reel kısmı Re(z)=2 ve imajiner kısmı Im(z)=3 tür. Z=5-2i karmaşık sayısında Re(z)=5 ve Im(z)=-2, Z=i karmaşık sayısında Re(z)=0 ve Im(z)=1, Z=7 karmaşık sayısında Re(z)=7 ve Im(z)=0 olur.
|
İ' nin kuvvetleri
|
|
|
Örnek1: Çözüm: Üsleri 4 e bölüp kalanlara bakarız. 34 ü 4 e
böldüğümüzde kalan 2 olduğundan 101 i 4
böldüğümüzde kalan 1 olduğundan 2016 yı 4
e böldüğümüzde kalan 0 olduğundan Toplam da
|
|
Örnek2:
Çözüm: Bu gibi üsleri ardışık olarak verilen i nin kuvvetlerinin ilk 4 terimi ve son terimi hesaplanır.
|
|
Örnek3:
İlk 4 terim toplamı sıfır olur. Bundan sonraki her 4 terim toplamı sıfır olur. En son geri kalan terim i ve ondan önceki terimler olur. i den önceki terimler olmadığından cevap sadece i olur.
|
|
Örnek4:
Çözüm: 4n ifadesi 4 ün katı anlamına geldiğinden, 4n+2 yi 4 e böldüğümüzde kalan 2 olur. Aynı şekilde 8n+1 ifadesinin 4 e bölümününden kalan 1 olur. Aynı mantıkla devam edersek 12n+3 ifadesinin 4 e bölümünden kalan 3 olur. Sonuç,
|
İki Karmaşık sayının eşitliği
|
İki
karmaşık sayı,
|
|
Örnek5:
eşitliğin sol tarafındaki reel kısım olan 2, sağ taraftaki reel kısım olan y sayısına eşittir ve y=2 bulunur. eşitliğin sol tarafındaki sanal kısım olan '(x+1), sağ tarafın sanal kısmı olan 5 sayısına eşittir. Buradan da, -(x+1)=5 ve x=-6 bulunur.
|
KARMAŞIK SAYININ EŞLENİĞİ
|
Dikkat: Sanal kısım işaret değiştiriyor. Noktanın x eksenine göre simetrisi alınır.
|
|
Örnek6: Aşağıdaki karmaşık sayıların eşleniğini bulalım,
|
|
Özellikler: 1) 2) 3) 4)
|
|
Örnek7:
|
|
Özellik:
|
|
Örnek8:
|
|
Örnek9:
Sonuç
|
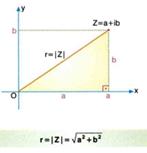
Bir Karmaşık Sayının Modülü (normu, uzunluğu, mutlak değeri, başlangıç noktasına olan uzunluğu)
|
Z=a+ib olan bir karmaşık sayının orjine olan uzaklığı şekilden de görüldüğü üzere Pisagor yapmak demektir.
|
|
Örnek10:
|
|
ÖZELLİKLER:
|
|
Örnek11:
|
|
Örnek12: 3-4-5, 6-8-10, 5-12-13 kenarlarını kullanabiliriz.
|
|
ÖSS Sorusu:
Buradan
b=-2 bulunur.
|
Yapılan Yorumlar
Soru olsa cozumu biz yapsak daha iyi ve ben bu konuyu cok seviyorum
Admin: ilginiz icin tesekkur ederim. Yeni bir siteyiz aklimizda o da var. Form da acacagiz ama yogunluktan bu donem yetistiremedik.
çok iyiii yaaaa
Bu siteyi cok sevdim tam bizim aradigimiz sekilde olmus kisa ve anlasilir sekilde cok tesekkurler
Çok beğendim. Teşekkürler.
Gerçekten tam bir yks öğrencisine anlatır düzeyde. Çok beğendim siteyi. Tekrardan teşekkürler.
TEŞEEKKKKÜRRRRLEEEER
Yorum Yapın
- Yüzde Problemleri - 2 (Kar - Zarar Problemleri) 321370 ziyaret
- İşçi Problemleri 293410 ziyaret
- EBOB - EKOK - 2 125468 ziyaret
- Karmaşık Sayılar 107941 ziyaret
- Polinomlar - 1 81482 ziyaret
- EBOB - EKOK - 2 2 dakika önce
- Polinomlar - 1 5 dakika önce
- 2. Dereceden Denklemler - 3 5 dakika önce
- Sayılar 6 dakika önce
- Sayılarla İlgili Karışık Örnekler 16 dakika önce