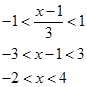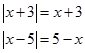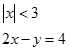1) , () şeklindeki denklemler.

 veya   dır.

Örnek1:  ise    veya  tür.

(sebebini  bilelim; sıfır noktasına olan uzaklığı 3 birim olan noktalar 3 ve -3 noktalarıdır.)

Örnek2:  ise   Ç.K.=?

Çözüm: olduğundan denklem  yani   olur.   Buradan da

 veya   olur. Buradan da ve  olur.  .

Örnek3:   ise Ç.K.=?

Çözüm: ve  (!) uzaklık negatif olamaz. (-1 metre şeklinde bir uzaklık duyan varmıJ

Dolayısıyla Ç.K.=

Örnek4:  denkleminin çözüm kümesini bulalım.

Çözüm4: Mutlak değerin içindeki ifade  5 veya -5 dir. Yani:  veya   dir. Buradan da;

i) veya  ii)  dir.

i için 1)  ve                                       ii için Ç.K.=  (bkz örnek3)

         2)  ve                    sonuç olarak Ç.K=  

ÖRNEK5:  denkleminin çözüm kümesini bulalım.

Çözüm5: Bu tip sorularda mutlak değerin içini sıfır yapan değerlere göre inceleme yapılır.

 içini sıfır yapan değer  0 olduğundan 1)    için ve  2)  için fonksiyon incelenir.

1)  için  olduğundan fonksiyon  ve  olur.

2) için  olduğundan fonksiyon  ve  olur. (!!)  kabul edip x=12 bulduk.

Dolayısıyla bu değer çözüm kümesine eklenmez. Sonuç   olur.

Örnek6)   sağlayan x değerleri toplamı kaçtır?

Çözüm: Sözü uzatmadan pratik verelim:   ve  olmak üzere x değerleri toplamı '2m' dir.

Soruya dönecek olursak , ifadesi her a değeri  için pozitif olduğundan verdiğimiz pratik bilgiye göre

Cevabımız mutlak değerin içini sıfır yapan değerin 2 katıdır. x-5=0 ve x=5 olduğundan cevap  dur.

2) ,  formatında eşitsizlikler.

 olur.

Örnek1:  çözüm kümesini bulalım.

Çözüm1:               olur. tam sayı  değerlerini sorsaydı cevap 11 olurdu.

Örnek2:  sağlayan x in alabileceği tam sayı değerleri toplamı kaçtır?

Çözüm2:         olur. değerlerin toplamı = olur.

Örnek3:  eşitsizliğini sağlayan x in alabileceği kaç farklı tam sayı değeri  vardır?

Çözüm3: İfadeyi  haline getirelim.

                                  -1,0,1,2,3 olmak üzere alabileceği 5 değer var gibi görünse de unutmamamız gereken bir durum var.  ifadesinde paydayı sıfır yapan değer (x=1) ifadeyi tanımsız

yapacağından kümeden çıkarılır. Yani -1,0,2,3 olmak üzere 4 değer  vardır.

3)  şeklindeki eşitsizlikler.

  veya    olur.

Örnek1:  ifadesinin çözüm kümesini bualım.

     veya           

Örnek2:   çözüm kümesini bulalım.

Arkadaşlar işlem yapmaya gerek yok. Tüm mutlak değerli ifadeler negatif bir sayıdan büyük olduğundan Ç.K:R

Örnek3:        olduğuna göre x in alabileceği kaç farklı tek sayı değeri vardır?

Çözüm3: ifadesinde mutlak değer içindeki ifade mutlak değer dışına olduğu gibi çıktığından mutlak değerin içi

Sıfırdan büyük veya eşit olmalı.                  .............(1)

 ifadesinde mutlak değer içindeki ifade dışarı işaret değiştirip çıktığından mutlak değer içindeki ifade

Sıfırdan küçük veya eşit olmalı.  ....................(2)

(1) ve (2) den sonuç    olur.  Tek tamsayılar istendiğinden  -3,-1,1,3,5 olmak üzere 5 değer vardır.

Örnek4:       ise, y nin en geniş çözüm kümesini bulalım.

Çözüm4: Bir eşitlik ve bir eşitsizlik verildiğinde eşitliği eşitsizlik yerine yazmak gerekir.

 ifadesini mutlak değer  ifadesindeki x yerine yazalım.  haline dönüşür. Buradan da (3.özellik

gereği)

                elde edilir. y nin çözüm kümesi   olur.