EŞİTSİZLİKLERDE DELTA (![]() ) KAVRAMI
) KAVRAMI
|
|
|
Örnek1: Çözüm:
Negatif
olan yerler
|
|
Örnek2: Çözüm: Yine
|
|
ÖYS SORUSU:
Çözüm:
|
EŞİTSİZLİK SİSTEMİ
|
Birden fazla eşitsizliğin oluşturduğu sisteme denir. Eşitsizliklerin her birini sağlayan değerleri, yani eşitsizliklerin kesişimini bulmaya çalışacağız.
|
|
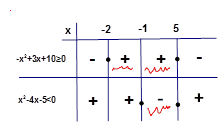
Örnek3:
İşaret tablosunu çizelim,
Burada dikkat edilmesi gereken eşitsizlik tablosunda işaretler denklemin kendi kökünde değişir. Yani
Benzer
şekilde x=-3 ,
|
|
Örnek4: Önce kökleri bulalım,
İşaret tablosunu yapalım.
|
|
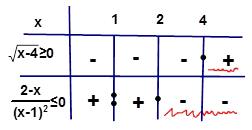
Örnek5: Çözüm: Kökleri bulalım.
Her iki
eşitsizliği sağlayan değerlerin
|
|
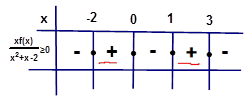
Örnek6:
Çözüm: Eşitsizliğin çarpanları olan denklemlerin köklerini bulalım.
Kökler x=0,
x=1, x=3 ve x=-2. Burada dikkat edilmesi gereken nokta x=-2 nin tek kat
olduğudur. Çünkü f(x) ten gelen çift kat kök ve İşaret tablosunu yapalım.
Tabloyu yaparken en önemli nokta 3 ten büyük değerler için (-) ile başlamak. Bunu da grafikten görüyoruz. Grafikte 3 ten büyük değerlerde f(x) negatif değerler alıyor. Eşitsizlikteki başkatsayılar da + olduğundan en sağ negatif ile başlar. Kökleri
incelersek, paydayı sıfır yapan x=-2 ve x=1 eşitsizliği sağlamazken, pay
kısmını sıfır yapan x=0 ve x=3 eşitsizliği sağlar ve bu yüzden çözüm kümesine
eklenir. Çözüm kümesi Tam sayılar
toplamı da
|

Eşitsizlikler - 1
Yapılan Yorumlar
Paydaki 2 değeri tek katlı kök paydadaki 2 değeri çift katlı kök ise 2 sayısı çözüm kümesine dahil edilir mi?
Admin: paydada olanlar çözüm kelimesine dahil edilmez.
gercekten cok faydali oldu tesekkur ederim
çok teşekkür ederim çok yardımcı oldunuz
sağolun faydalı kısa ve öz
Çok faydalı sonsuz teşekkür
Cidden teşekkürler 😊
Çok işe yaradı
Çok sagolun elinize emeginize sağlık
Teşekkürler
nerden geldiğini bilmesek de çok faydalı olmuş teşekkürler..
Yorum Yapın
- Yüzde Problemleri - 2 (Kar - Zarar Problemleri) 321354 ziyaret
- 2. Dereceden Denklemler - 1 157074 ziyaret
- EBOB - EKOK - 2 125391 ziyaret
- Faktoriyel 503377 ziyaret
- EBOB - EKOK - 1 127351 ziyaret
- Basit Eşitsizlikler 11 dakika önce
- Mutlak Değer - 1 19 dakika önce
- 2. Dereceden Denklemler - 1 19 dakika önce
- Sayı Kesir Problemleri - 1 31 dakika önce
- EBOB - EKOK - 1 45 dakika önce
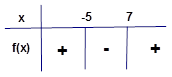
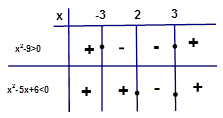
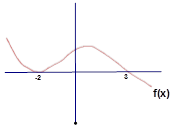 Şekilde
Şekilde