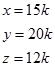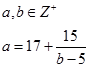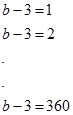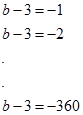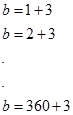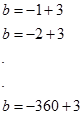1) olmak üzere ise

a)x+y en çok kaçtır?

b)x+y en az kaçtır?

Arkadaşlar bu sorularda dikkat etmemiz gereken en önemli şey sayıların hangi kümeye ait olduğudur.( bu soruda ) bu kalıp soruların çözümünde x,y ikililerin birbirine yakın ve uzak değerleri incelenir.

Çarpımları 20 olan birbirine en yakın iki pozitif sayı 4 ve 5 tir. Toplamları 9.

Çarpımları 20 olan birbirine en uzak iki pozitif sayı 1 ve 20 dir. Toplamları 21.

Dolayısıyla a)x+y en çok 21 ve b)x+y en az 9 olur.

2) olmak üzere ise

a)x+y en çok kaçtır?

b)x+y en az kaçtır?

Aynı kalıp soru olup çözüm yolu ilk örneğin aynıdır.

a)En yakın olan (-6)ve (-5) değerleri için toplam (-11) olur.

b)En uzak olan (-1) ve (-30) değerleri için toplam (-31) olur.

!İlk örnekte birbirine yakın değerler en küçük değeri verirken ikinci örnekte en büyük değeri verdi. Bu soru kalıbında değerleri yakın mı uzak mı vereceğiz diye düşünmekten ise hem yakın hem en uzak değerleri verip değerlendirelim.

3-) ve ise

a) x.y en çok kaçtır?

b)x.y en az kaçtır?

Bu soru kalıbında da muhabbetimiz aynı olacak. Yani en yakın ve en uzak değerler....

Toplamları 16 olan birbirine en yakın iki dğal sayı sayı (eşit alırız) (8) ve(8) dir. (dikkat: sayılar farklı dememiş)

Toplamları 16 olan birbirine en uzak iki doğal sayı (0) ve (16) dır. (dikkat: 1 ve 15 alınmadı. Doğal sayılar sıfır sayısından başlar )

Sonuç: 8 ve 8 için x.y=64

0 ve 16 için x.y=0 olur. a)en çok= 64 b) en az=0

4)(3. sorunun benzeri)

, olmak üzere ise

x.y nin alabileceği en büyük ve en küçük değerlerleri bulalım.

Birbirlerine en yakın iki sayı (7)ve (9)dur.(dikkat: olduğu için) çarpımları da (7.9=63) olur.

Birbirlerine en uzak iki sayı (1) ve (15) dir. (dikkat: 0 alınmadı olduğu için.) çarpımları da (1.15=15) olur.

x.y nin alabileceği en büyük değer 63, en küçük değer de 15 dir.

* 5-)(3.sorunun zoru)

ve ise x.y en çok kaçtır.

dendiği için x ve y değişkenlerine değer veremeyiz. Toplamların en büyük olması için sayıların birbirine en yakın (mümkünse eşit) olması gerekir .(bkz örnek3) yani alırız. Ve sonuç: olur.

6)(Biraz daha zoru)

ve olmak üzere

ise A.B ifadesinin alabileceği en büyük değer kaçtır?

Yukarıdaki örnekler anlaşıldıysa bu soruda da A=B sağlanması gerektiğini yorumlayabiliriz.

A=B ise buradan da çıkar. x değerini A veya B ifadesinde yazarsak

Buradan çıkar. en büyük değerdir.

7)

ve ise alabileceği en küçük değer kaçtır?

Bu kalıptaki sorularda dikkat etmemiz gereken, orantılardaki aynı değişkenlerin (bu soruda y değişkeni) eşit olduğunu bilmemizdir.

İlk eşitlikte x=3k ve y=4k dersek ikinci eşitlikte y=5m ve z=3m dersek y değeri sabit olacağından 4k=5m olmalı.

Dolayısıyla y, 4 ve 5 in bir katı olmalı. Eşitlikleri y=20k olacak şekilde genişletmek gerekir.

. = ve .= olur. olur. k en az 1 olur. ()

olur. (not:bu soruda en büyük değer sorulmaz. Sizce neden?)

8-) şartını sağlayan kaç a değeri vardır?

sonra haline getirelim. Sonra 'çıkmış soru1' deki çözüm yolunu kullanırsak

Paydanın yani (b-5) ifadesinin 15'i bölen bir sayı olması gerekir.

1.durum: ve 2.durum seçilir. 2.durum için a ifadesi negatif değerler alacağından ( olmalı)incelemeye gerek kalmaz. 1.durum için b, 4 değer alacağı için a da 4 değer alır.

(değerlerin kaç olduğunu istemediği için incelemeyip cevap 4 tür diyeceğiz.)

9)(8 in biraz zoru)

ise a nın kaç değeri vardır?

1.durum: ve 2.durum seçilir. Bu soruda gözden kaçırmamamız gereken şey 2.durumdaki 4 değeri de paydaya versek a yine pozitif değerler alır. Ama tüm değerleri veremeyiz çünkü b nin de pozitif olma durumunu değerlendirmeliyiz.

ve olur. Dolayısıyla 1.durumdan 4 değer ve 2. durumdan 2 değer olmak üzere a nın

alabileceği 6 değer vardır.

*10)(kendinizi zorlayın)

eşitliğini sağlayan b değerleri toplamı kaçtır?

haline getirdik. Paydanın 360 sayısını bölmesi gerektiğini biliyoruz artık. 360 sayısını bölen

sayıları bu sefer tek tek yazamayız. Bunun için formülümüz var. 360 ı çarpanlarına ayırırsak;

ve tam bölenleri sayısı: dir. (!Bunların 24 ü pozitif diğer 24'ü de bu sayıların negatifidir.)

(360'ın bölenlerinin sayısını obeb-okek konusunda ayrıntılı işleyeceğiz.)

Paydanın yani (b-3) ün alabileceği 48 değer vardır. 48 değeri de (b-3) ifadesine eşitlediğimizi düşünelim.

ve buradan b nin değerlerini alt alta yazıp toplayalım. ve

Dikkat edilirse bölenlerin negatifleri olduğundan birbirini götürür ve geriye sadece 3 ler kalır. Peki kaç tane 3? Tabi ki bölen sayısı kadar. Yani 48 tane 3. Cevap: 48.3=144.