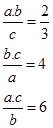Tanım: Aynı birimdeki  iki çokluğun birbirine bölümüne oran denir.

a nın b ye oranı a:b veya  () şeklinde gösterilir.

Örnek1: Ayhan'ın boyu 1.70 m, Ahmet'in boyu  180 cm ise Ayhan'ın boyunun Ahmet'in boyuna oranı kaçtır?

Çözüm1: eğer  dersek yanlış olur. birimlerin aynı olması gerektiğinden birimleri eşitlemek gerekir. 

1.70 m=170cm olduğundan cevap  olur.

ÖSS sorusu:   olduğuna göre  nin değeri kaçtır?

Çözüm: a gördüğümüz yere -2b yazalım.

 bulunur.

Tanım: İki veya daha fazla oranın eşitliğine orantı denir.

A) eşitliğine ikili orantı denir.

. Bu eşitlikteki k ya orantı sabiti denir.

.a ya 1.terim, b ye 2. terim, c ye 3. terim, d ye 4. terim denir.

.d ye sırası ile a,b,c sayılarının 4. orantılısı denir.

.  ifadesi a:b=c:d şeklinde de gösterilir. Bu ifadede b ve c içler, a ve d dışlar olarak tanımlanır. Bu nedenle

b.c=a.d çarpımına içler dışlar çarpımı denir.

Örnek2:   ise

Çözüm2: Verilen ifadede içler dışlar çarpımı yaparsak:

6x-3y=2x+4y, buradan da 4x=7y elde edilir. Sonra  x=7k ve y=4k alınıp istenen ifadede yerine yazılırsa;

 elde edilir.

Örnek3:  2,3,8 sayılarıyla dördüncü orantılı sayıyı bulalım.

Çözüm3: dördüncü orantılı sayı x olsun.

 bulunur.

B)  eşitliğine üçlü orantı denir.   ifadesi   şeklinde de gösterilir.

Örnek4)   a:1:6=2:4:b orantısına göre a+b=?

Çözüm4)  şeklinde yazar içler dışlar çarpımı yaparsak ;

4a=2 ve a=1/2 bulunur. aynı şekilde 1.b=24 ve b=24 bulunur. a+b=1/2+24=49/2 bulunur.

Özellik1)  orantısında    dır.

Örnek5:   ve  ise b=?

Çözüm5: =k   orantı sabitini eklersek.              elde ederiz. Verilen eşitlikte bu ifadeleri yazalım.

3.2k-3k+2.4k=33 buradan 11k=33 ve k=3 elde edilir. b=3k olduğundan b=3.3=9 bulunur.

Özellik2)Bir orantıda oranların payları toplamı, paydaların toplamına bölünürse orantı sabiti değişmez. Yani;

  ise  olur.

Örnek6: =5  ise   olur.

Özellik3:  ve  özellik2 gereği   olur.

!Yani bir orantıda oranların paylarını belli sayılarla çarpıp toplar ve aynı işlemi oranların payda kısmına da uygularsak orantı sabiti değişmez.

Örnek7:  ise  olur

Örnek8:  ve  ise z=?

1.yol: a terimi 3, b terimi (-1) ile çarpılıp toplanmış. Bizde aynı şekilde 2 yi 3 ile ve 3 ü (-1) ile çarpalım.

 elde edilir.

2.yol:Çözüm5 mantığı ile çözebiliriz.

 diyelim. Buradan   elde edilir.  ifadesinde yerine yazarsak;

 ve z=4k olduğundan z=4.3=12 bulunur.

*Örnek9:  ve    veriliyor.  b değerini bulalım.

Çözüm9: a terimi 3 ile, c terimi, (-2) ile ve e  terimi 1 ile çarpılıp toplanmış. Aynı işlemi biz pay için uygulayalım. Yani

b terimini 3 ile, d terimini (-2) ile ve f terimini 1 ile çarpıp toplarsak, orantı sabiti değişmeyecek.

 olur. verilenleri yerine yazarsak,  elde ederiz. İçler dışlar çarpımı yaparsak,

 bulunur.

Özellik4:  orantısında  olur.

Örnek10:  ve  ise a kaçtır?

Çözüm10:   olsun    olur. buradan da  bulunur.

 bulunur.

Özelik5: ise  olur. aynı şekilde  ise  olur.

Örnek11:  ise   oranı kaç olur?

Çözüm11:  bulunur.

Örnek12:   ise   ifadeleri taraf tarafa çarparsak,  

 bulunur. 

Örnek13: x,y ve z maddelerinden oluşan 370 gr lık bir  karışımda,  ve   oranları varsa bu karışımda kaç gram x maddesi vardır?

Çözüm13: (bu sorunun benzeri sayılar karışık örnekler soru 7 de çözüldü).

Bu soruda önemli olan y teriminin gördüğü sayıları eşitlemektir. Birinci orantıda y=3k iken ikinci orantıda y=5m gibi değer alır. Bu değerleri eşitlemek gerekir. Bunun için birinci orantıyı  5 ile ikinci orantıyı 3 ile genişletelim.

= ve   = bulunur. buradan x=10k, y=15k ve z=12k elde edilir. karışım miktarı

370 gr olduğundan, x+y+z=10k+15k+12k=370 , 37k=370,  k=10 bulunur. x=10k olduğundan x=10.10=100 gr bulunur.